√無料でダウンロード！ 平行 四辺 形 証明 問題 340216

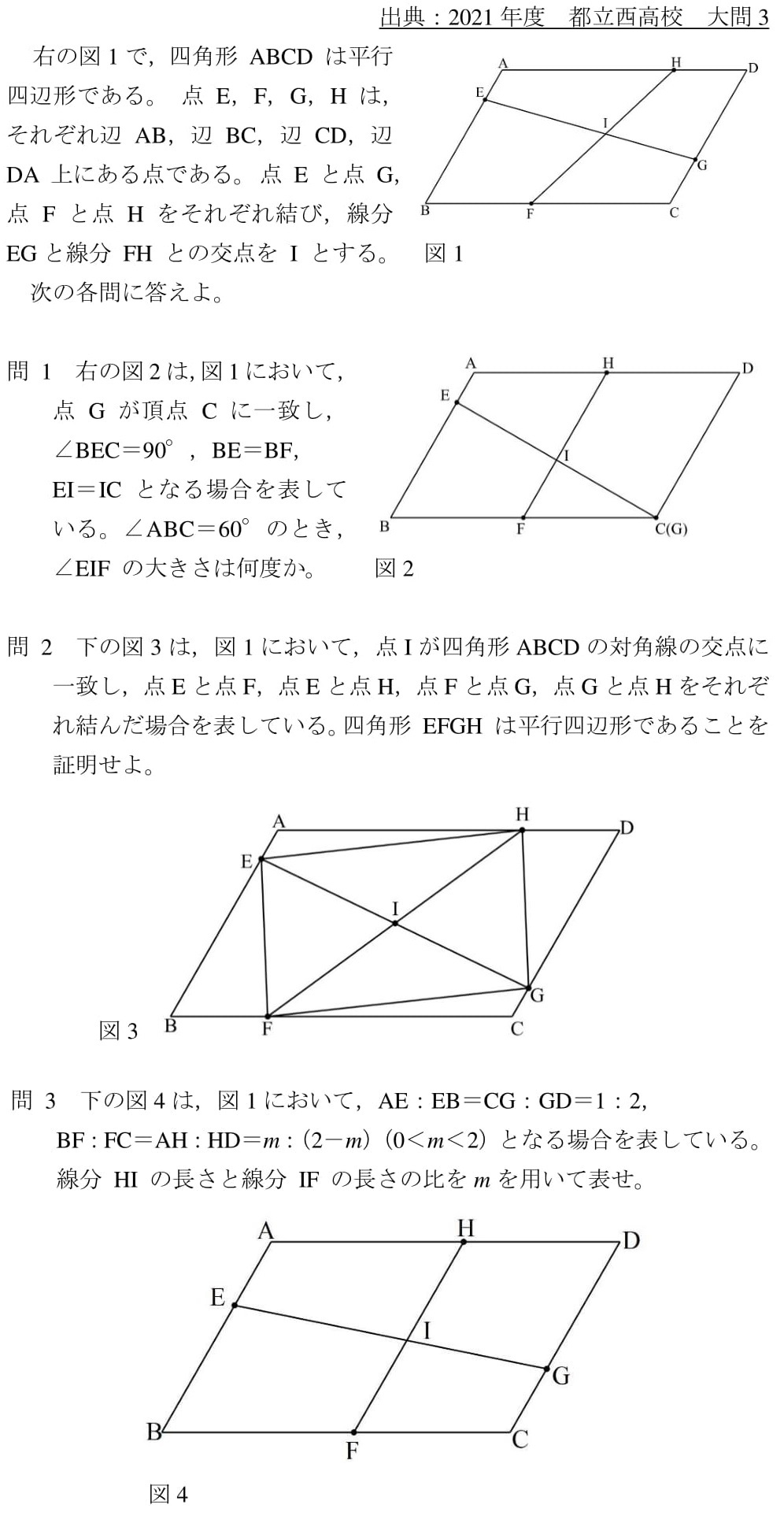
21都立西 平行四辺形の難問証明 高校入試 数学 良問 難問

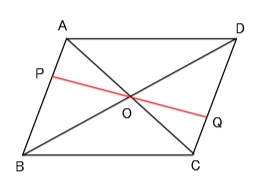
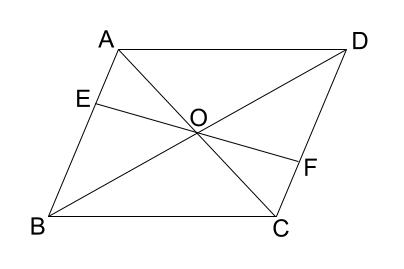
平行四辺形の証明「問題に挑戦」の証明に誤りがあると思います。 eo＝foであることを証明せよ、という問題です。 証明の3行目 eo＝fo・・・① となっていますが、 正しくは、oa＝ocではないでしょうか。 さらに証明の8行目 平行四辺形の性質 長さ・角度の問題 平行四辺形の性質と長さや角度を求める問題です。 平行四辺形の性質は小学校で習ったものと同じですが、証明で使えるように定義、性質、条件などを自分で説明できるようにしっかり理解するようにしてください。

平行 四辺 形 証明 問題

平行 四辺 形 証明 問題-平行線や角の性質、それに基づいた図形の性質の理解をもとにして、三角形や多角形などの角の値を求める練習ができる問題プリントです。 合同と証明 練習問題 （1） 答え 合同と証明 練習問題 （2） 答え 合同と証明 練習問題 （3） 答え 合同と証明2年生 5 図形の性質と証明 知識・技能の習得を図る問題 年 組 号 氏名 全国学力・学習状況調査 A問題 ② 2 下のように「平行四辺形の2組の向かい合う辺はそれぞれ等しい」ことを証明しました。

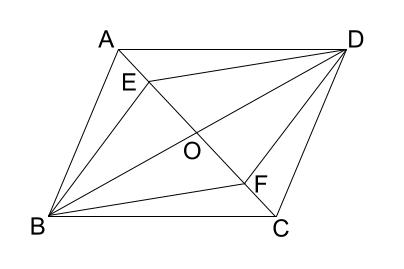
中学数学 平行四辺形になることの証明 その１ 中学数学の無料オンライン学習サイトchu Su

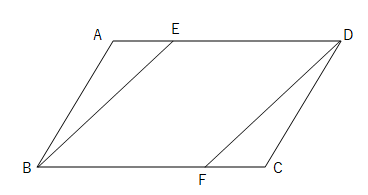
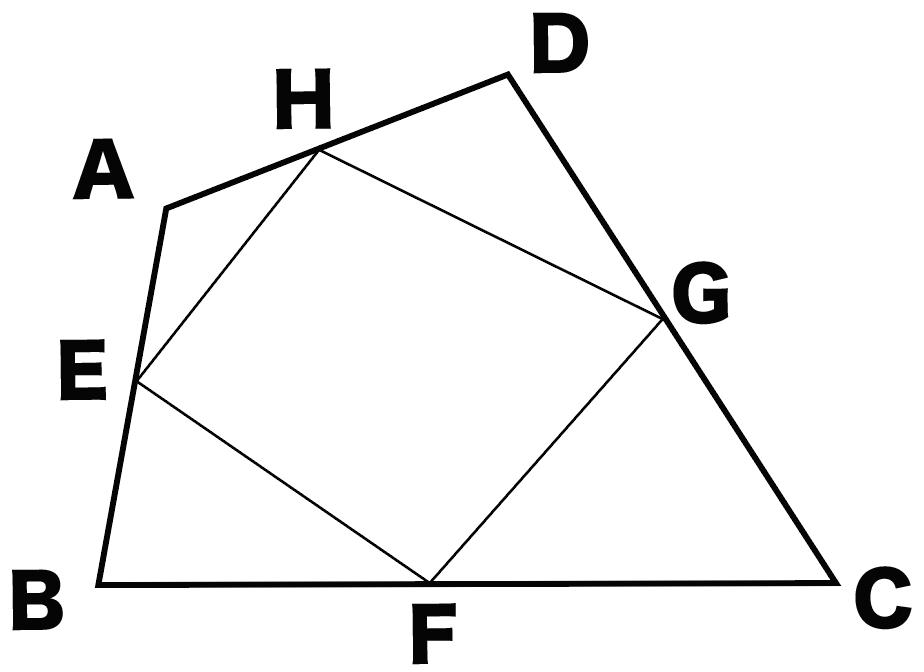
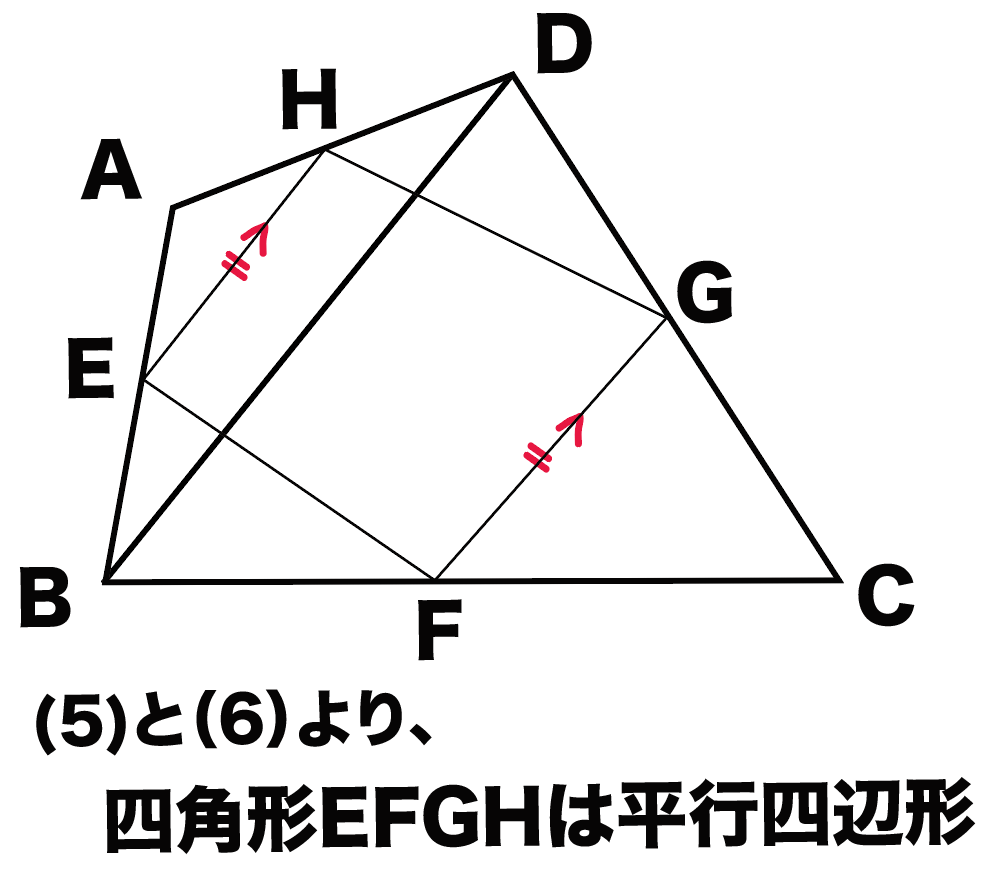
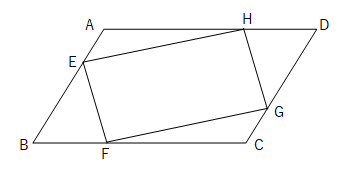
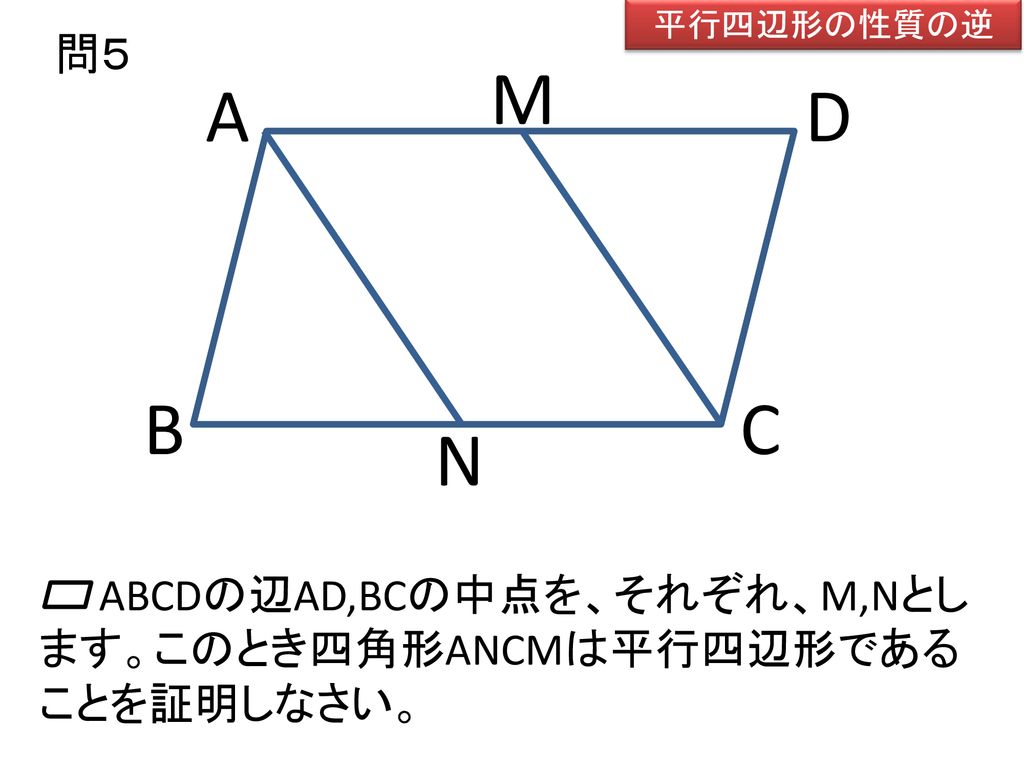
 平行四辺形の練習問題（平行四辺形になることの証明） 平行四辺形abcdの辺ab,cd,da上に,それぞれ,点e,f,g,hを,ae＝cg,bf＝dhとなるようにとります。このとき,四角形efghは,どんな四角形になりますか。証明し答えなさい。 平行四辺形解答2 aehと cgf において 仮定より7．平行四辺形の証明問題 ①2組の向かいあう辺が、それぞれ平行な四角形（とき） ＜定義＞ （条件） ②2組の向かいあう辺が、それぞれ等しい（とき） ＜性質＞（条件） 練習問題③「平行四辺形であることを証明する」 中点連結定理とは、 三角形の \(2\) 辺のそれぞれの中点を結んだ線分について成り立つ定理 です。 中点連結定理

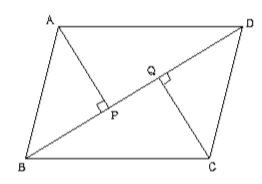
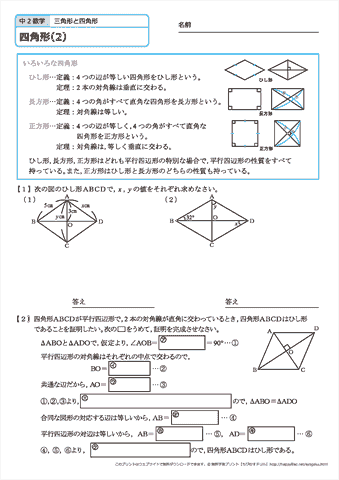
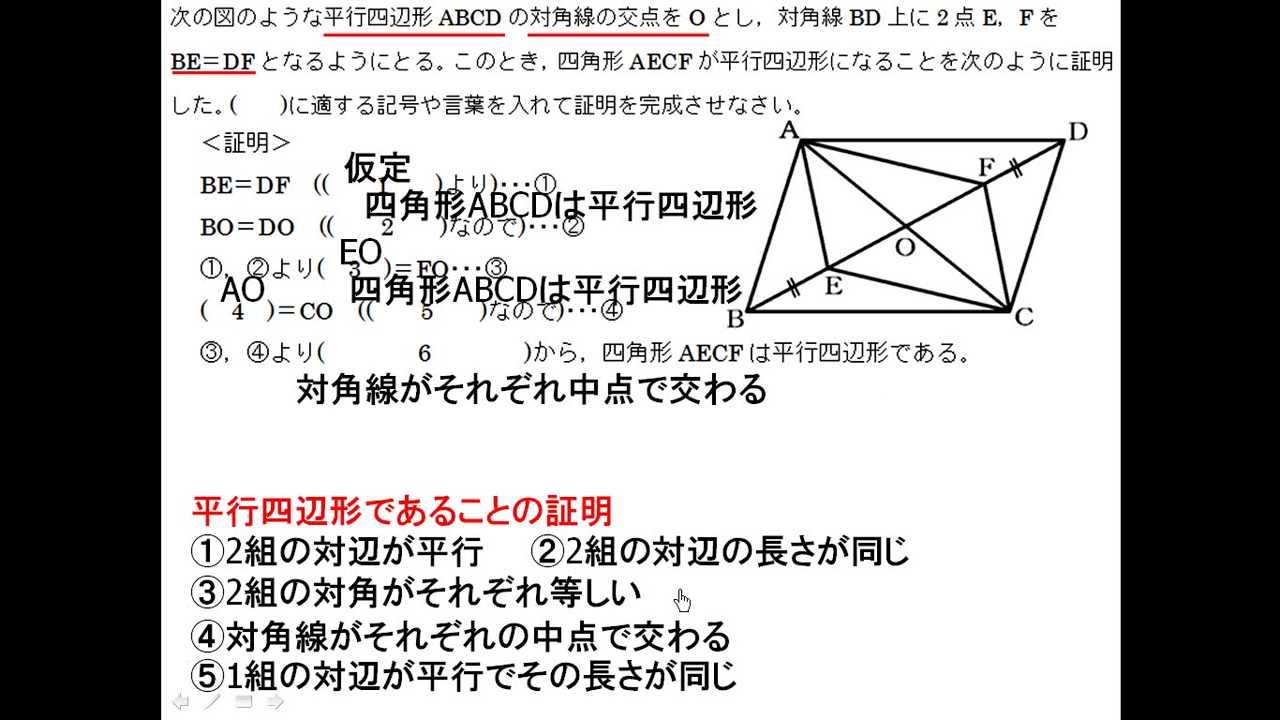
 平行四辺形になる条件は、言葉だけでなく図形とセットで覚えるのがポイントです。 では、以上のことを踏まえて次の問題を解いてみましょう。 問題：次の(1)～(4)のうち、平行四辺形であるといえるものを選びなさい。 (1) ad=5 ㎝、bc＝5 ㎝、ab//cd の四角形 abcd 平行四辺形の証明 練習問題1 下図の平行四辺形abcdで, 対角線bd上に、2点e、fをbe=dfとなるようにとります。このとき, ae = cfであることを証明せよ 解答1平行四辺形になると思うよ。 僕がかいた図でも，平行四辺形にみえるよ。 四角形EBFDはどんな四角形になりそうですか。図をかいてみましょう。 「四角形EBFDは平行四辺形になる」という結論を示すために，何がわかればよいですか。

平行 四辺 形 証明 問題のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「平行 四辺 形 証明 問題」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「平行 四辺 形 証明 問題」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「平行 四辺 形 証明 問題」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「平行 四辺 形 証明 問題」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「平行 四辺 形 証明 問題」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「平行 四辺 形 証明 問題」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「平行 四辺 形 証明 問題」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「平行 四辺 形 証明 問題」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「平行 四辺 形 証明 問題」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「平行 四辺 形 証明 問題」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「平行 四辺 形 証明 問題」の画像ギャラリー、詳細は各画像をクリックしてください。

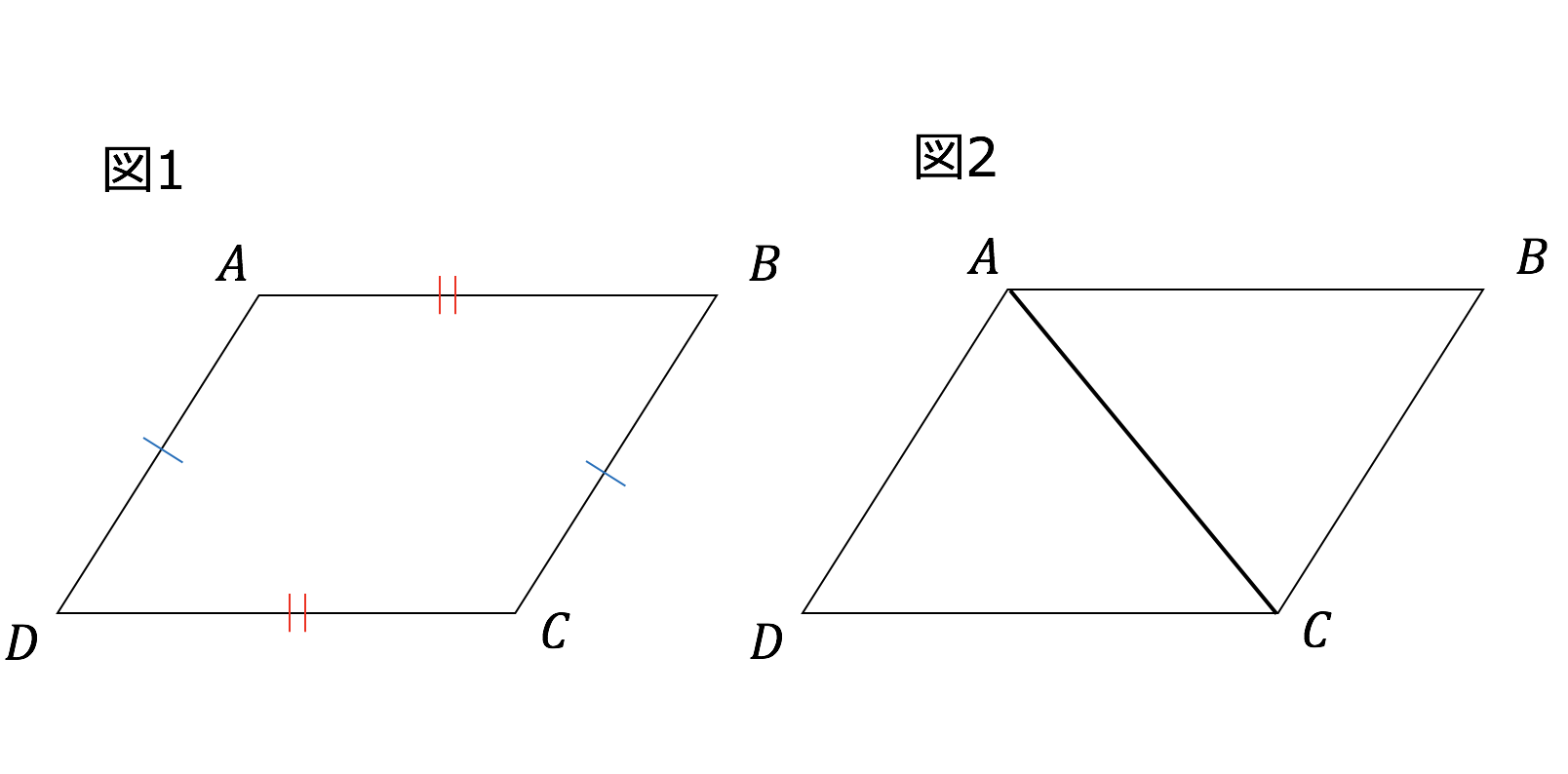 マジック 中学全学年 平行四辺形になる条件 証明 合同条件 平行四辺形 直角三角形 三角形の合同 平行四辺形になる条件 このノートが参考になったら、著者をフォローをしませんか？ 気軽に新しいノートをチェックすることができます！以上で二つのベクトルが作る平行四辺形の面積は、それらのベクトル積の大きさに等しいことがわかりました。 ベクトル \(\overrightarrow{a} = \langle2, 0, 0 \rangle\) と \(\overrightarrow{b} = \langle 1, 1, 0 \rangle\) が作る平行四辺形の面積を求めよ。